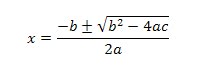Buenas tardes apreciados estudiantes la siguiente publicación es para recupera la 1ra clase que correspondía al día 26 de marzo
Ecuación de Primer Grado
Ecuación de Primer Grado
Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable, y que se cumple para determinado valor numérico de dicha incógnita.
Se denominan ecuaciones lineales o de primer grado a las igualdades algebraicas con incógnitas cuyo exponente es 1 (elevadas a uno, que no se escribe).
Como procedimiento general para resolver ecuaciones enteras de primer grado se deben seguir los siguientes pasos:
1. Se reducen los términos semejantes, cuando es posible.
2. Se hace la transposición de términos (aplicando inverso aditivo o multiplicativo), los que contengan la incógnita se ubican en el miembro izquierdo, y los que carezcan de ella en el derecho.
3. Se reducen términos semejantes, hasta donde es posible.
4. Se despeja la incógnita, dividiendo ambos miembros de la ecuación por el coeficiente de la incógnita (inverso multiplicativo), y se simplifica.
Resolución de ecuaciones de primer grado con una incógnita
Para resolver ecuaciones de primer grado con una incógnita, aplicamos el criterio del operador inverso (inverso aditivo o inverso multiplicativo), como veremos en el siguiente ejemplo:
Resolver la ecuación 2x – 3 = 53
Debemos tener las letras a un lado y los números al otro lado de la igualdad (=), entonces para llevar el –3 al otro lado de la igualdad, le aplicamos el inverso aditivo (el inverso aditivo de –3 es +3, porque la operación inversa de la resta es la suma).
Entonces hacemos:
2x – 3 + 3 = 53 + 3
En el primer miembro –3 se elimina con +3 y tendremos:
2x = 53 + 3
2x = 56
Ahora tenemos el número 2 que está multiplicando a la variable o incógnita x, entonces lo pasaremos al otro lado de la igualdad dividiendo. Para hacerlo, aplicamos el inverso multiplicativo de 2 (que es ½) a ambos lados de la ecuación:
2x • ½ = 56 • ½
Simplificamos y tendremos ahora:
x = 56 / 2
x = 28
Ejemplo
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.
Quitamos paréntesis, agrupamos y sumamos los términos semejantes:
Despejamos la incógnita:
Solución a la ecuación de segundo grado
La siguiente expresión es una ecuación de 2do grado, siempre y cuando el coeficiente a≠0.
La mayoría de las personas utilizamos la famosa resolvente de la ecuación de 2do grado, es decir:
para obtener así las raíces o también llamadas soluciones. Pero muchos aceptamos esta resolvente como un dogma y pocos nos preocupamos por investigar de donde sale esa expresión que garantiza la solución a la ecuación de segundo grado. Para los curiosos y los que no lo son voy a resolverles y explicarle los pasos para llegar a la resolvente de segundo grado.
1 1) Vamos aplicar la técnica de completación de cuadrados, es necesario saberla de lo contrario se te hará un poco difícil entender los pasos siguientes,
Completación de cuadrados.
En esta oportunidad vamos a explicar la técnica de completación de cuadrados, técnica útil en varias áreas de las matemáticas, Para comprender mejor este método, nos enfocaremos primero en las ecuaciones del tipo
Aunque esta técnica no se limita a este tipo de expresiones. Los siguientes pasos van a estar enfocados en expresiones cuadráticas de la forma x^2 + bx + c = 0, o sea, cuando el coeficiente a = 1. En los ejemplos posteriores a estos pasos se mostrará cómo trabajar cuando a≠1. Es sencillo, así que no te preocupes.
Pasos para realizar la completación de cuadrados.
· Se selecciona el valor absoluto del término b, es decir, aunque este término sea negativo siempre lo tomaras positivo.
· Divides este término por 2 y a esa expresión la elevas al cuadrado. Ejemplo (b/2)^2.
· Suma y resta este nuevo término a la expresión dada.
· El primer término agregado se simplifica, osea, se simplifica la fracción que está dentro del paréntesis siempre y cuando esto sea posible, el segundo término se desarrolla.
· A los tres primeros términos se le completa cuadrado, a los dos últimos se le realizan operaciones.
· Para completar cuadrados se procede como sigue; se le calcula la raíz cuadrada al primer término, luego coloca el signo del término b, seguido de la raíz cuadrada del tercer término, que justamente va ser la expresión simplificada dentro del paréntesis. Toda esta expresión que calculaste se eleva al cuadrado.
· Ambas expresiones, la resultante de los tres primeros términos y la de los dos últimos será tu completación de cuadrados.